
| Genre: | Maths Tutor |
| Publisher: | LCL |
| Cover Art Language: | English |
| Machine Compatibility: | BBC Model B, BBC Model B+, BBC Master 128, Acorn Electron |
| Release: | Professionally released on Cassette |
| Available For: | Amstrad CPC464 & BBC/Electron |
| Compatible Emulators: | BeebEm (PC (Windows)) PcBBC (PC (MS-DOS)) Model B Emulator (PC (Windows)) Elkulator 1.0 (PC (Windows)) |
| Original Release Date: | 1st January 1984 |
| Original Release Price: | £9.99 |
| Market Valuation: | £2.50 (How Is This Calculated?) |
| Item Weight: | 64g |
| Box Type: | Cassette Single Plastic Clear |
| Author(s): | Genevieve Ludinski |
Variant Items
There are 2 other items featuring this same game (that we know about!). Click any of them for their details.
Active Auctions
Closed Auctions
Buy It
Unfortunately no-one is currently selling this item.
Auction Price Watch
Worried you're being ripped off? Closing prices on eBay can help you decide what a reasonable price is for a particular item.
Full Instructions
Blurb
Mega Maths is an A-Level step-by-step, self-tuition and revision course, for mature beginners, A-Level students and Micro Maths users.
The course contains 24 programs with extensive graphics on 105 topics, held on two tapes or discs, with two books. It was designed and tested by A-Level Maths teachers, and written by a professional programmer.
It takes the user from simple topics, such as permutations and straight line geometry to advanced topics such as integral calculus. It covers the topics common to "Pure Maths" and "Pure and Applied Maths" A-Levels and many others. Pure Maths topics are taught and tested using LCL's highly-acclaimed step-by-step method, as used in Micro Maths, while other topics are tested.
Each program includes instructions, an unlimited number of problems, and complete explanations for wrong answers. In most versions the computer can turn into a calculator at any time during the program run and return to the problem when required. The 105 topics are common to all the examining boards, i.e.:
- Permutations and combinations
- Straight line geometry
- Circle geometry
- Operations on polynomials
- Applications of the Remainder Theorem
- Inequalities
- Logarithms
- Three-dimensional geometry
- Solution of quadratic equations by formula
- Complex number
- Operations on roots of equations
- Derivation of equations from roots
- Arithmetic and geometric progressions
- Applications of the Binomial Theorem
- Standard deritvatives
- Derivative of functions of a function, products and quotients
- Tangents and normals to curves
- Maxima, minima and stationary points of graphs
- Trigonometry of large angles and special angles
- Trigonometical graphs
- Trigonometical identities
- Partial fractions
- Standard integrals
- Integration of function of a function, powers of trigonometrical functions by partial fractions, using trig. identities and by parts
- Applications of integral calculus
Loading Instructions
LCL Mega Maths teaches, and sets and marks an infinite number of problems on the subjects of the GCE A-Level course. It is designed to be used in schools and colleges as a Computer-assisted learning aid, or as a self-tuition and revision course. It is written for the BBC Micro (Model B and B+) and the Electron.
It is a sequel to Micro Maths which is a complete course taking students from age 8 years upwards to O-Level standard. Mega Maths is designed for those who have completed Micro Maths and for A-level students needing extra help. However it can be used by mature beginners, as everything the user needs to know is included in the coourse, though being A-Level it would be too difficult for most children. It covers the subjects common to the A-Level 'Pure Maths' and 'Pure and Applied Maths' exams and many others. 105 topics are covered by manual and computer, the rest by manual.
To load and run the course select a disc or tape and key in CHAIN"MENU" then press RETURN. The MENU must be CHAINed before using any programs as it contains vital information required by the programs.
Operating Instructions
Each program first sets you a problem. If the answer is a number then omit any units, for example, key in 4.9 not 4.9 cm. If the answer is alphanumeric (i.e. a mixture of letters and numbers) then omit any unnecessary spaces, brackets, addition signs and zeroes preceding whole numbers. For example, key in X+2 not (+X +02). Use ^ to represent 'to the power of' so X^2 is X squared. Note that capital X represents the letter X. Little x is only used in the explanations to represent the multiplication sign and you should not use it in a response. Remember, throughout all the programs to press the RETURN key after keying in the required response. If you have no idea of what the required response should be, then just press the RETURN key.
If you get the answer right, it is ticked and then you are asked 'Do you want more (Y/N)'. If you press Y (or just RETURN) another problem is displayed. If you press N, the program ends. Only this method may be used for ending a program. The disc version then returns you to the menu while the tape version takes you to the next program.
If you get the answer wrong, you are given a hint or told how to do that kind of problem. If you get it right this time, the program proceeds as described above. If not, the correct answer is given followed by a complete explanation. Then the program proceeds as described above.
Calculator Mode
If you require a calculator to calculate the result of a problem then press ?(RETURN) to enter the Calculator mode. In this mode, the computer acts like a calculation. For example, to add numbers 12 and 39 just key in:
12+39=
The operators are:
+,-,* (multiply),/ (divide), ^ (to the power of), SQR (square root of)
In the Calculator mode the 'calculator' is switched to radians so the trigonometrical functions of an angle such as 45 degrees are:
SIN(45*DG),COS(45*DG),TAN(45*DG) or ATN(0.1)/DG
where ATN stands for arctangent.
Brackets may also be used. As in a calculator, key in AC(RETURN) to clear the calculator display, and key in - to display the result. No answer is displayed if you have made any typing errors, so clear the display and try again. To exit the Calculator mode key in ? again.
Menu
There is a Menu program on each tape or disc and it must be CHAINed first. Once loaded the title page is displayed, pressing any key will cause this to be replaced by the menu. For tape versions remember to press the STOP button on your tape recorder when the selected program starts if you do not have a remote-controlled recorder.
MEGA MATHS 1
Permutations
A permutation is an arrangement of items. The permutations of P, A and T are:
PAT,PTA,APT,ATP,TPA,TAP
4! is called 4 factorial and is 4x3x2x1 = 24.
The exception is zero factorial which equals 1. If you are working out how many different towers of bricks you can make from 3 bricks, the top brick in the tower can be any of the 3 bricks. For each top brick the second brick can be one of 2 (as you have used one up) and the third brick can only be the one left. So the number of permutations is 3x2x1. See the permutations above of PAT to prove this. If the tower could only have 1 brick the number of permutations would be 3. At the end of each problem this is illustrated. The program covers permutations with items that can and can not be used repeatedly.
Combinations
A combinations is an arragement of items where their order in the arrangement is not important. For example, the number of combinations of 3 bricks labelled P, A and T in groups of 2 bricks are (P & A),(A & T) and (P & T). This program covers combinations and permutations with some identical items.
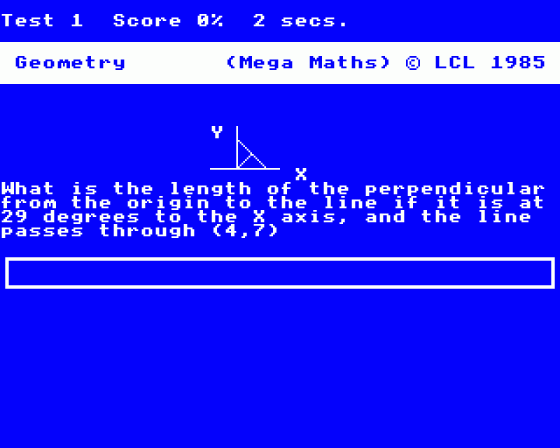
Straight Line Geometry
It is assumed you know that a straight line has the equation Y=mX+c where m is the gradient of the line and c is a constant. This covers the derivation of the equation given the intercepts on the X and Y axes, and given the gradient and a point the line passes through.
Circle Geometry
This covers problems on coordinate Geometry of a circle, and one type of problem on straight line Geometry. The straight line questions require the equation of the straight line to be derived when the length of a perpendicular from the origin to the line, and the angle between the perpendicular and the X axis is given. The circle Geometry problems cover the derivation of the centre and radius from its equation, and the derivation of the equation of the circle given its centre and radius. Also it covers the derivation of the equation of a tangent to a circle, whose equation is given, at a given point.
Polynomials and Remainder Theorem
This covers the addition and subtraction of polynomials and problems on the application of the Remainder Theorem.
Inequalities
This covers the application of the rules of inequations. Remember > is 'greater than' and < is 'less than'. It covers the rules of adding, subtracting, multiplying or dividing each side by a positive or negative constant. It also covers the application of the rules of adding, or subtracting another variable whose range is known. You can not assume the rules of inequations are the same as the rules of inequations are the same as the rules for ordinary equations and this teaches you which are the same and which are not.
Logarithms
If A-102 then the Log. of A to the base 10 is equal to 2 or log10(A)-2 to a power and changing the bases of numbers.
Three-dimensional Geometry
This program covers two-dimensional problems using angles of elevation and depression, compass directions and bearings, and three-dimensional problems. In the two-dimensional problems press @ to represent ° (symbol for degrees). In three-dimensional problems knowledge of Pythagoras Theorem and the arctangent rule is used. Arctangent is the opposite of tangent, so if tan(A) = opposite/adjacent then arctab(opposite/adjacent) = A.
Solution of Quadratic Equations
This covers the solution of quadratic equations where the result can not easily be obtained by factorisation and equating each 'bracket' to zero.
Complex Numbers
This program includes addition, subtraction, multiplication and division of complex numbers and their moduli. Complex conjugates are also explained.
Operations on Roots of Quadratics
This includes the addition and multiplication of roots of a quadratic equation. It also covers the derivation of a quadratic equation given the sum and product of its roots. Key in the answer to the questions on the sum or product of roots as a proper or improper fraction, so key in 1/2, 7/4 instead of 0.5 and 1.7.
Arithmetic and Geometric Series
This program includes the calculation of a term in an Arithmetic series, the calculation of the difference in an Arithmetic series, the calculation of the sum of a given number of terms in an Arithmetic series, and the calculation of the sum of an infinite number of terms in a Geometric series. An example of an Arithmetic series is 1+3+5+7... note the difference is 2 in this case. An example of a Geometric series is 3+6+12+24...
Binomial Theorem
This covers the evaluation of an expression to 1 decimal place using the Binomial Theorem and the calculation of a given term in a Binomial series.
MEGA MATHS 2
Standard Derivatives
To differentiate, you need to know the standard derivatives which are taught and tested in this program. Learn the derivative of sinX (=cosX) and remember that the derivative of cosX is the opposite in sign (=-sinX). You must learn the rest. Differentiation is used to find the gradient of a curve at any point, or the rate of change of a property varying with time (such as velocity) or space, for example. The program also covers the product and quotient of two functions of X. The derivative of terms added (or subtracted) together is the sum (or difference) of the derivative of each term.
Derivative of Functions
This includes the derivative of a function of a function of X, and the derivative of equations which include products of X and Y.
Tangents and Normals of Curves
This illustrates one of the applications of differentiation. You can find the gradient at any point on a curve by differentiating the equation and substituting the coordinates of that point for X and Y. This will also be the gradient of the tangent to the curve at that point. As you know the gradient of the tangent and a point it goes through, you can derive its equation. This program also covers finding the equation of a normal to a curve at a given point.
Maxima and Minima
This is another illustration of the uses of differntial calculus. As you travel left to right along an 'n' shaped curve, the gradient goes from positive, to zero at the top, to negative on the downward side of the curve. Therefore to find the position of the stationary point at the top, differentiate the equation of the curve to get the gradient and equate it to zero. As in this 'n' shaped curve the gradient is going from positive to negative the gradient is decreasing so the rate of change of the gradient will be negative. In a 'u' shaped curve the gradient goes from negative to positive, so the gradient is increasing, or the rate of change of the gradient is positive. So if you differentiate the equation of a curve twice, its sign after substitution of X and Y will indicate if the curve is a 'u' shape (i.e. has a minimum) or an 'n' shape (i.e. has a maximum). The program covers the determination of the stationary point and the shape of the curve.
Trigonometry of Large Angles
Angles are measured in an anti-clockwise direction from the positive X axis. They can be measured in units of either degrees or radians. There are 180° (degrees) between two ends of a straight line or ϖ radiants (ϖ = 22/7). The sign of the trigonometrical function of an angle, that is the sin, cos or tan, depends on which quardrant it is in. The trig, function of all angles between 0 and 90° is positive. The sine of all angles between 90 and 180° is positive, but the cos and tan of these angles is negative. Similarly the tan of all angles between 180 and 270° is positive, while the other trig. functions are negative. For angles between 270 and 360° the cosines is positive, but the other functions are negative.
This program covers the trigonometry of large angles and special angles. In the questions on special angles press the red function key f0 for the square root symbol, and key in he answer in fraction form, e.g. key in √3/2 not 0.86. This is to ensure you have not cheated and used the calculator mode!
Do not try and learn the trig. functions of special angles by heart, but derive them each time using the methods described below. Consider a square of side length 1, by Pythagoras Theorem, the hypothenuse is √ 1 + 1 = √2. Since the sin of an angle in a right-angled triangle = opposite/hypotenuse, cos = adjacent/hypotenuse and tan = opposite/adjacent, you can work out the sin, cos and tan of 45°. See Figure 1.
Consider a triangle whose sides are all equal and of size 180°/3 = 60°. If you drop a perpendicular down from the top, as shown in Figure 2, it will bisect the angle it cuts and the triangle base.
Since the length of each triangle side is 2, applying Pythagoras Theorem the length of the perpendicular is √22-12 = √3, so you can now work out sin, cos and tan of 30° and 60°.
Consider the rotating radii of unit length in Figure 3. A right-angled triangle is formed by dropping a perpendicular from the end of the radius to the horizontal axis. If the radius moves just slightly from 0°, the case of the triangle will be approximately 1 and the height approximately 0. As the angle approaches 0°, the base and height become 1 and 0 so the sin, cos and tan of 0° can be derived. Consider, now, a radius approaching 90°, similarly the height of this triangle approaches 1 and base approaches 0 so the sin, cos and tan or 90° can be derived.
IMAGE MISSING
Trigonometrical graphs
This covers the calculation of the Y coordinate of a point on a sine and cosine curve, given the X coordinate in radians. If you can calculate the coordinates on points on the curve you can draw it. This can be used to solve an equation containing a trig. function. Draw two graphs, one for each expression either side of the equation, and the value of the variable at the point of intersection is the solution of the equation. Graph paper is supplied which can be used, photocoped if necessary, to plot the two graphs, then key in the X coordinate of the point of intersection.
Watch the sine and cosine waves displayed on the screen. You will see that sine waves with no phase angle, such as sin(2X), pass through the origin at the midpoint of the upward slope, while cosine waves with no phase angle, such as cos(2X), intersect the Y axis at its peak. A sine or cosine wave with a phase angle, such sin(2X+20°), shifts the wave along the X axis in the opposite direction, so a phase angle of +20° shifts it by 20° to the left.
Trigonometrical Identities
This tests the trig. identities which must be learnt. If you learn sin(A+B), cos(A+B) and tan(A+B) identities, then you can derive sin(A-B), cos(A-B) and tan(A-B) by rewriting them as sin(A+(-B)) etc. Remember sin(-A)=-sin(A) and the cosine equivalent is, as usual, the opposite, i.e. cos(-A)=cos(A). Thus tan(-A)=sin(-A)/cos(-A)=-tan(A) You can work out sin2A, cos2A and tan2A from sin(A+A) etc.
This program assumes you can factorise. Remember to factorise X2+aX+b, work out by trial and error two positive or negative numbers whose product is b and whose sum is a. If you call these numbers r and s, the expression can be rewritten (X+r)(X+s).
Partial Fractions
This program covers the derivation of partial fractions, from Algebraic fractions with linear and quadratic terms in the denominator.
Standard Integrals
Remember the derivative of sinX is cosX, well the integral of sin X is the opposite (i.e. =-cosX). Having discovered the integral of sinX, you can find the integral of the others as they are the opposite of the derivatives.
Integration of Functions
You are advised to complete the programs 'Trigonometrical identities' and 'Partial Fractions' before attempting this program. Before you integrate a more complicated function of X you must work out which method to use. This program helps you learn to identify which method to use, and once you have found the method you can apply it then integrate using standard integrals. This program covers integration by parts, and integration of a function of a function of X. Also integration using partial fractions, and using trig. identities for even and odd powers of sinX and cosX, powers of tanX, and products in the form sinAXcosBX.
The trig. identities used are versions of the ones covered, so:
cos(2X) = cos(X+X) = cosX cosX - sinX sinX
= cos2 - sin2X
and this can be converted to only sin2X or only cosX terms using the identity sin2X+cos2X=1. If you divide this identity by cos2X you get: 1 + tan2X = sec2X.
Sometimes more than one method must be applied to integrate a function. If so, key in the method letters in the order they must be applied using the fewest number of methods possible.
Uses of Integration
The integral of Y with respect to X over a range of X is the sum of all the values of Y in that range of X. This can be seen in this program as the area under the curve is made up of an infinite number or vertical lines of height Y over that range of X. This program shows what integration is and what it is used for. It covers the calculation of the area under a curve, and the area enclosed by two lines, the X axis and a curve taking account of positive and negative areas.
Glossary
ACUTE ANGLE. An angle less than 90°.
CONSTANT. A quantity that does not vary.
GRADIENT. The slope, or ratio of the vertical distance to the horizontal distance.
HYPOTENUSE. The side opposite the right-angle in a right-angled triangle.
INTERCEPT. The point of intersection.
ORIGIN. The point of intersection of the axes, i.e. (0,0)
PERPENDICULAR. Straight line making an angle of 90° with another line or plane.
QUADRATIC EQUATION. Equation with a variable to the power of 2.
ROOTS of an equation. Value of the unknown quantity that satisfies the equation.
SERIES. Sum of a set of terms in a defined order with a rule for obtaining each term.
Screen Designers
The following utilities are also available to allow you to edit the supplied screens of this game:
Cheats
Download
A digital version of this item can be downloaded right here at Everygamegoing (All our downloads are in .zip format).
| Download | What It Contains |
|---|---|
| A digital version of Mega Maths suitable for BeebEm (PC (Windows)), PcBBC (PC (MS-DOS)), Model B Emulator (PC (Windows)), Elkulator 1.0 (PC (Windows)) |
Report A Problem
We thank you from the bottom of our hearts if you report something wrong on our site. It's the only way we can fix any problems!
You are not currently logged in so your report will be anonymous.
Add Note
Release Country
Change the country to update it. Click outside of this pop-up to cancel.
Scan Of Selected Article
If you auction an item, it will no longer show in the regular shop section of the site.









